小5 算数 ロイロノートを活用し拡散的思考、収束的思考を促す【実践事例】(新潟県聖籠町立山倉小学校)
| 授業担当者 | 山澤 晴子 |
| ICT環境 | 1人1台タブレット |
| 学年 / 教科 | 小学校5年/算数 |
| 単元 | 図形の面積 |
〈実践の概要〉
本単元では、三角形、平行四辺形、ひし形、台形、それぞれの面積を扱う。それぞれの図形の求積において、拡散的思考から収束的思考へとつなげる展開を構想した。具体的には、拡散的思考としては「図形を他の図形に変形させて求積する」、収束的思考としては「変形前後それぞれの図形の部分の長さに着目させ、求積の公式を導き出す」が挙げられる。それぞれの思考場面において、ロイロノートの活用が有効であった。
〈ロイロノート・スクール導入の効果・メリット〉
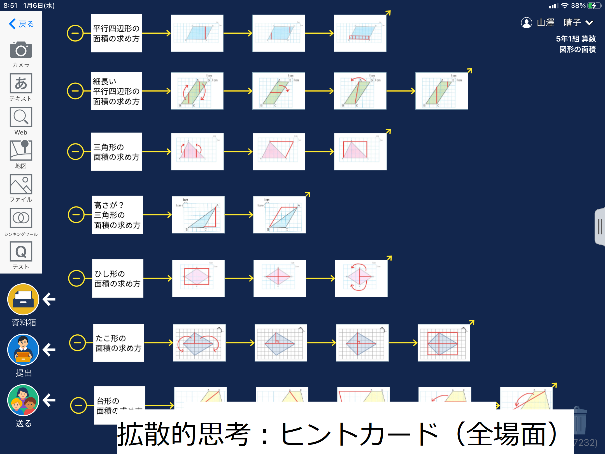
教師が資料箱にヒントカードを予め用意することにより、すべての児童が自力解決に向かうことができる。
児童は、即時に互いの考えを共有することができる。
教師は、児童の複数の考えから着目させたい考えを即時に選択でき、容易に児童に示すことができる。
〈実践の目標〉
三角形、平行四辺形、ひし形、台形の面積の計算による求め方について理解する。
図形を構成する要素などに着目して、基本図形の面積の求め方を見いだすとともに、その表現を振り返り、簡潔かつ的確な表現に高め、公式として導く。
〈授業写真〉

〈場面1〉平行四辺形の面積は、どのようにすれば求められるか
①拡散的思考場面
教師は、1㎝方眼用紙上に示された平行四辺形を提示し、面積は何㎠になるかを児童に問うた。児童は、1㎠マスを数えれば分かるとすぐに考えたものの、1㎠マスに入らない半端な部分をどう処理すればよいか迷っていた。この半端な部分の処理を全体の課題とし、まずは各自で自力解決をさせた。その際、どうしても自力解決できない児童がいた。そこで、教師は予め用意しておいたヒントカードを、必要な児童に対し、ロイロノートで配信することにより、児童全員が自分の考えをもてるようにした。
②収束的思考場面
その後、教師は、ロイロノートを使って、各自の考えを共有させた。さらに、それぞれの共通点を問うた。児童は、それぞれの考えを比較する中で、「平行四辺形の分割の方法は様々であるが、平行四辺形の面積は、平行四辺形を長方形や正方形に変形すれば求められる」という考えに収束していった。さらに、長方形の縦と平行四辺形の高さ、長方形の横と平行四辺形の底辺、それぞれが対応することを捉え、公式「平行四辺形の面積=底辺×高さ」を導き出すことができた。
〈場面2〉細長い平行四辺形の面積は、どのようにすれば求められるか
「細長い平行四辺形」とは、高さが外にある平行四辺形である。教師は、これまで(高さが内にある)とは違うということを意識付けさせるために、授業の導入として、練習問題をロイロノートに配信し、各自がどのようにして解いたかを画面で共有させた。その結果、児童は、平行四辺形の面積は「底辺×高さ」で求められる既習事項を確認した。そこで、教師は本時の課題につながる「細長い平行四辺形」を提示し、面積が何㎠になるかを問うた。その結果、児童は「どこが高さになるのか」という課題をもった。その後、児童は既習を想起し、長方形に変形する中で、「平行四辺形の高さは、向かい合った上下の辺の間の距離である」という考えに収束していった。
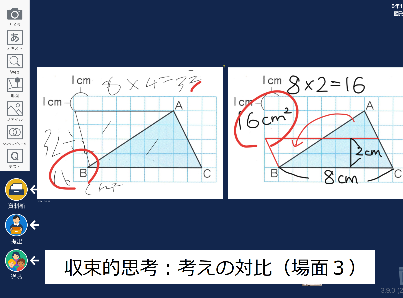
〈場面3〉三角形の面積は、どのようにすれば求められるか
①拡散的思考場面
教師は、1㎝方眼用紙上に示された三角形を提示し、面積は何㎠になるかを児童に問うた。児童は、既習を想起し、長方形や平行四辺形に変形すればよいと考えた。まずは各自で自力解決をさせた。その際、今回も教師は予め用意しておいたヒントカードをロイロノートで配信することにより、児童全員が自分の考えをもてるようにした。
②収束的思考場面
その後、教師は、ロイロノートや黒板を使って、各自の考えを共有させた。さらに、教師は児童の考えのうち、「倍積で平行四辺形に変形させたもの」「等積だが高さを2分の1にして平行四辺形に変形させたもの」を対比させ、公式を考えさせた。その結果、児童は、公式「三角形の面積=底辺×高さ÷2」を導き出すことができた。
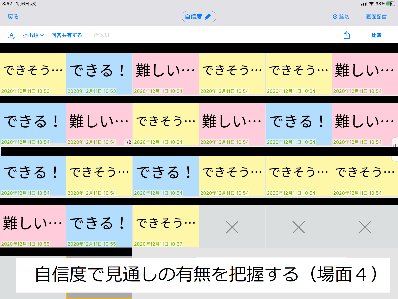
〈場面4〉高さが外にある三角形の面積は、どのようにすれば求められるか
教師は「高さが外にある三角形」を提示し、面積が何㎠になるかを問うた。ここでも、どこが高さになるかが課題となった。児童の反応からかなりの難問であることが感じられたので、教師はどの程度の児童が見通しをもっているかを把握する「自信度」を問うた。自信度はロイロノートの3色のカードを用いた。桃色「難しい」、黄色「できそう」、水色「できる」である。教師は、即時に自信度を把握し、水色カードを提出した児童を指名し、解決の糸口を全体で共有した。解決の糸口は、「平行四辺形の学習と同じように、三角形を他の形に変形すると高さが分かるのではないか」というものだった。その結果、児童は、「倍積で平行四辺形に変形すると、高さが平行四辺形の内にでき、この高さを三角形の高さと捉えられる」という考えに収束していった。
〈場面5〉ひし形の面積、台形の面積は、どのようにすれば求められるか
①拡散的思考場面
教師は、1㎝方眼用紙上に示されたひし形を提示し、面積は何㎠になるかを児童に問うた。児童は、既習を想起し、既習の図形に変形すればよいと考えた。今回も教師は予め用意しておいたヒントカードをロイロノートに配信することにより、児童全員が考えをもてるようにした。その結果、児童は、平行四辺形や三角形の学習を想起し求積することができた。
②収束的思考場面
児童の考えは「倍積で長方形に変形する」「等積で長方形に変形する」「等積で平行四辺形に変形する」の3つに大別された。そこで、教師はロイロノート上に3つの考えを対比させた。さらに、3つの共通点を問うことにより、児童は「どのような図形に変形させても、ひし形では対角線の長さを使って面積を求めている」という考えに収束していった。その結果、児童は、公式「ひし形の面積=対角線×対角線÷2」を導き出すことができた。
さらに、台形の面積においても、①「既習の図形に変形して面積を求める」、②「上底・下底と同じ部分を見つける」、③「公式を導き出す」の順に学習を進め、理解を深めていった。
〈場面6〉単元を通した学習を振り返る
単元のまとめとして、これまでどのような流れで学習が進んだのかを振り返らせた。その際、ロイロノートを活用し、各自がこれまで作成したカードを取捨選択させ、それらを時系列でつなげさせた。カードをつなぐ活動を通し、児童はそれぞれの場面で自分の考えがどう変容していったのかを想起することができた。
〈授業写真〉