高2 数学 微分法と積分法 数学Ⅱの微分法の学習における反転授業の試みについて【実践事例】(愛知県立熱田高等学校)
| 授業担当者 | 辻村 博 |
| ICT環境 | 1人1台タブレット |
| 学年 / 教科 | 第2学年/数学Ⅱ |
| 単元 | 微分法と積分法 |
〈実践の概要〉
高等学校の微分法の学習は感覚に訴えながら授業を進めざるを得ない。そこで,イメージを持って授業に臨めるように反転授業を試みた。微分法では増減表の意味を,積分法では微分と積分の関係及び面積を求めるための考え方についての動画を事前に閲覧した上で授業に参加するという形をとった。今回活用したものは,「探究学舎」によるYOUTUBE動画であり,1本5分程度なので生徒の負担にもならない。その動画のリンクを配付し,授業までに閲覧するように指示した。
〈ロイロノート・スクール導入の効果・メリット〉
反転学習が容易に実施できる。
授業時間を効率的に活用できる。
自分のペースでじっくり家庭学習ができる。
〈実践の目標〉
反転授業により,理解を促進する。
他教科でも反転授業が導入できるようにする。
〈授業写真〉
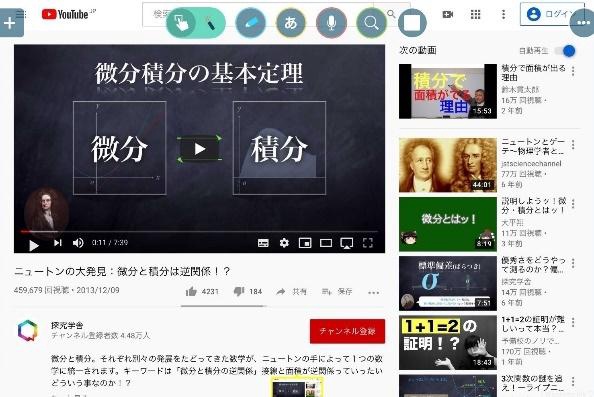

〈場面1〉ロイロノートの準備
動画を閲覧できるように準備をし,ロイロのノートで配信する。その際動画の意味,何に注意して閲覧するかを指示できるようにしておく。
〈場面2〉授業の流れ
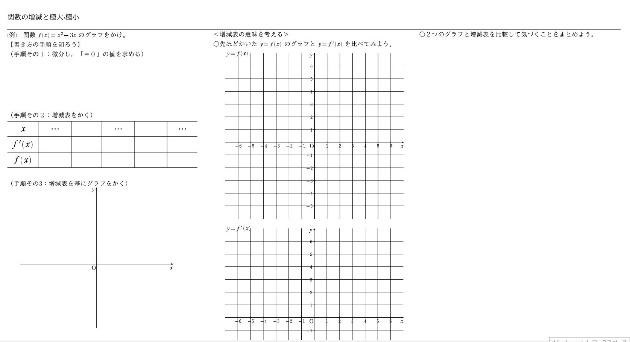
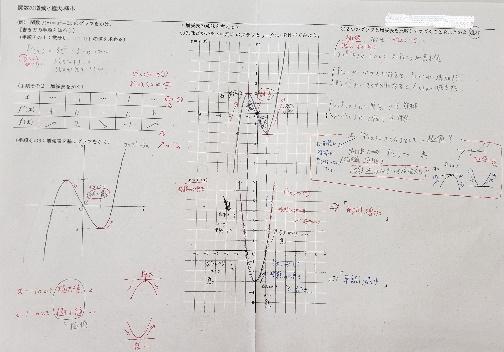
動画を閲覧したか確認し,その上で授業を進める。増減表の書き方,それを用いたグラフの書き方の手順を解説した上で,その増減表が何を表すかを確認する。また,授業の最後には再度動画で本時の学習内容を振り返り,増減表の意義を理解するように促す。その後,ロイロノートのアンケート機能を利用して,本時の自己評価と何を学んだかの言語化を実施した。
授業でわかったことをまとめさせたが,その一部を紹介する。
導関数のグラフではy座標が0より大きいと緩やかな傾きから急な傾きになって,0より小さいと急な傾きから緩やかな傾きになる。極値は導関数が0になるがその逆は成り立たない。成り立つときは極値の前後で傾きが右上がりか右下がりになるときのみ。傾きの方向が同じ時(右上がり・右上がり)は極値はない。
3次関数のグラフはNのような形になる。
〈授業写真〉