高1 数学 二次関数の値の変化 二次関数の最大と最小 数学Ⅰ 二次関数【授業案】日本大学豊山女子高等学校 篠原 大生
| 学年 / 教科: | 高1 数学 |
| 単元: | 数学Ⅰ 二次関数 |
| 指導要領: | 二次関数の値の変化 二次関数の最大と最小 |
| 教科書: | 数学Ⅱ |
| 授業者: | 篠原 大生(日本大学豊山女子高等学校) |
単元の一部
解説動画
この授業案のインポート用ノートデータ
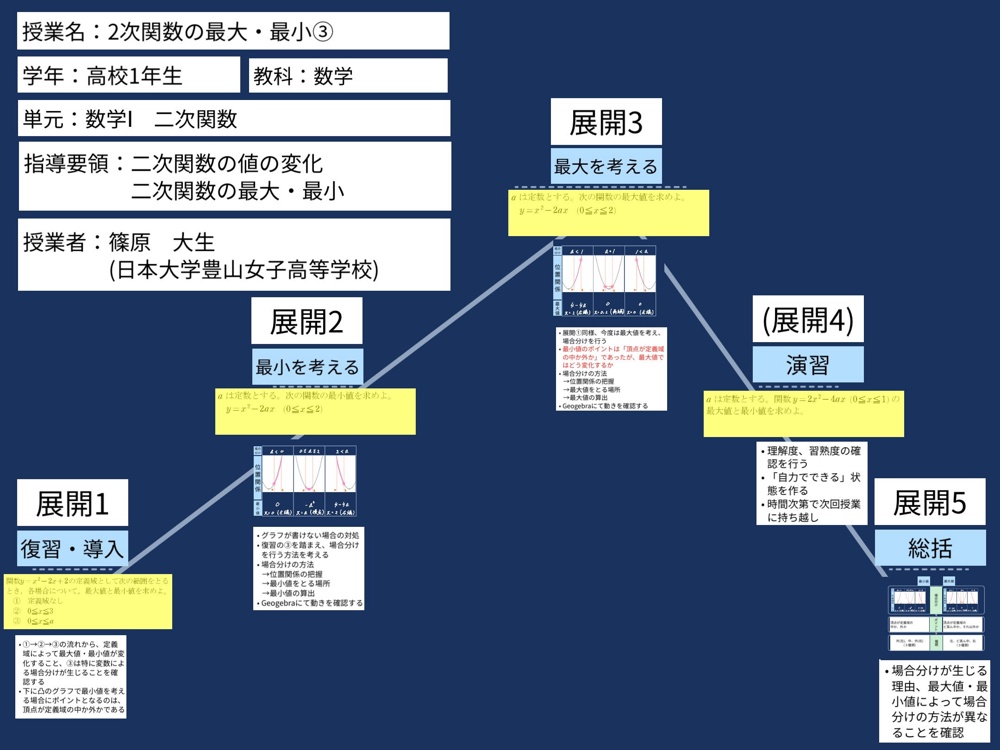
【展開1】復讐・導入
例題の定義域として、①定義域なし ②0≦x≦3 ③0≦x≦aのそれぞれについて最大値と最小値をもとめる。
・①→②→③の流れから、定義域によって最大値・最小値が変化すること、③は特に変数による場合分けが生じることを確認する。
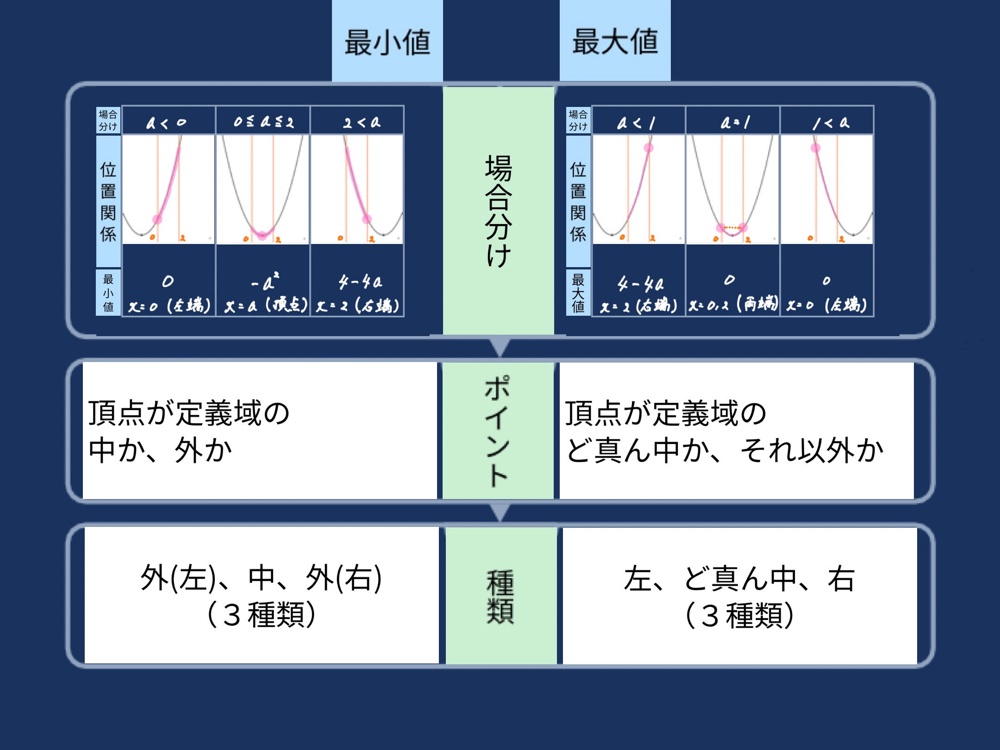
・下に凸のグラフで最小値を考える場合にポイントとなるのは、頂点が定義域の中か外かである。

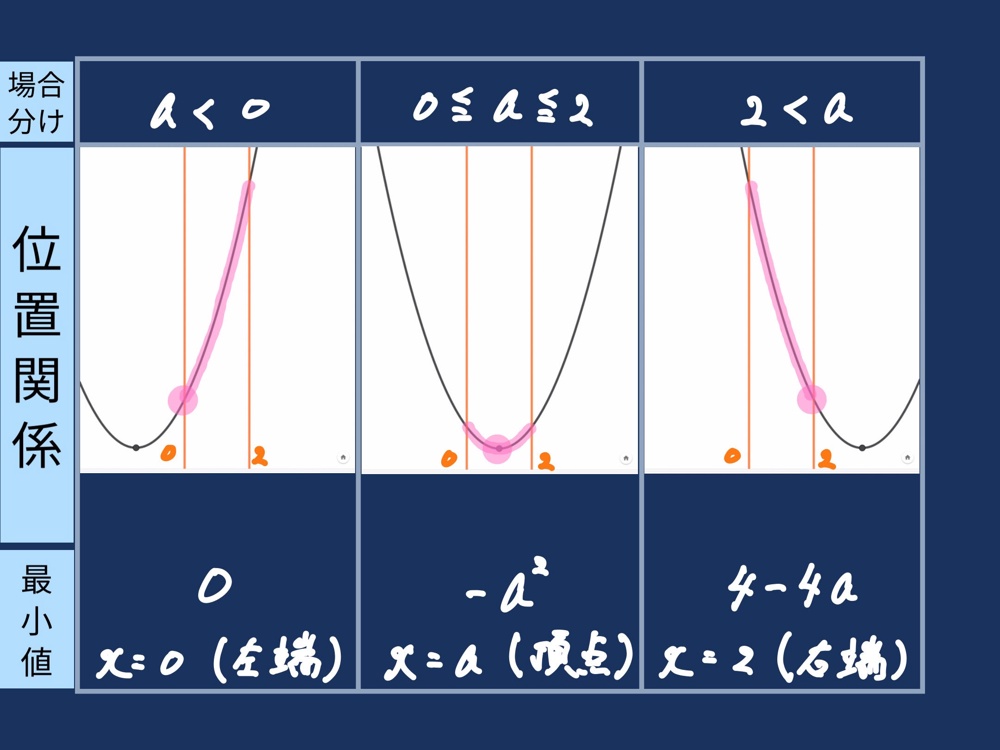
【展開2】最小を考える
例題について、グラフを書かせる。
グラフが書けない場合の対処
•展開1の③を踏まえ、場合分けを行う方法を考える。
•場合分けの方法
→位置関係の把握
→最小値をとる場所
→最小値の算出
•Geogebraにて動きを確認する。
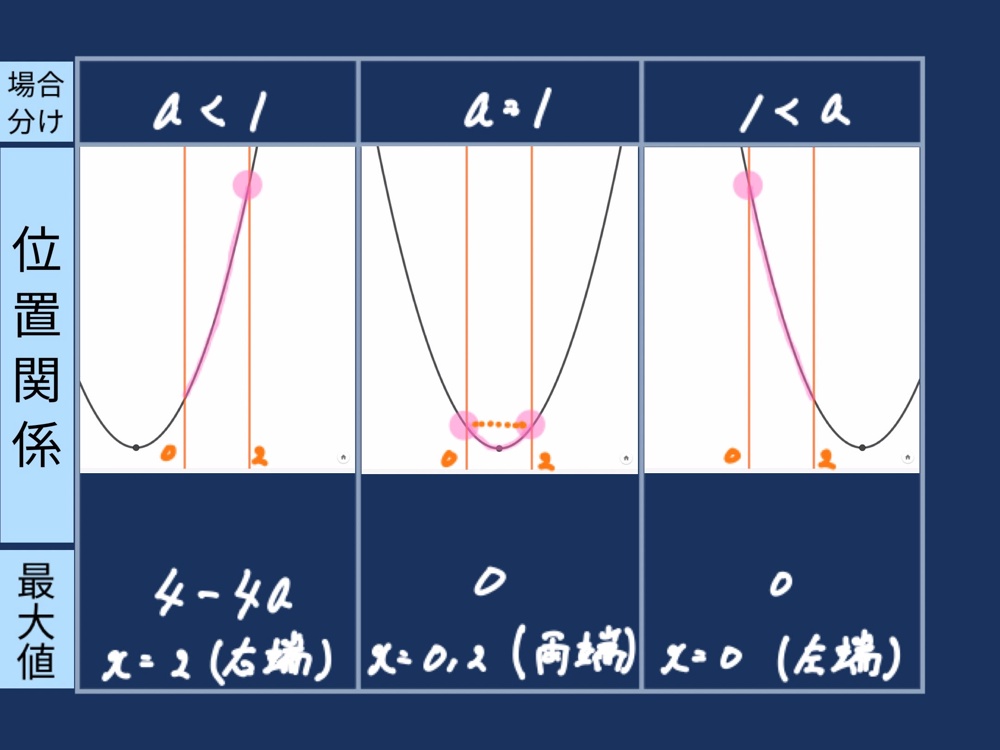
【展開3】最大を考える
展開①同様、今度は最大値を考え、場合分けを行う。
•最小値のポイントは「頂点が定義域の中か外か」であったが、最大値ではどう変化するか。
•場合分けの方法
→位置関係の把握
→最大値をとる場所
→最大値の算出
•Geogebraにて動きを確認する。
【展開4】演習
•理解度、習熟度の確認を行う。
•「自力でできる」状態を作る。
•時間次第で次回授業に持ち越し。

【展開5】総括
場合分けが生じる理由、最大値・最小値によって場合分けの方法が異なることを確認。