高1 数学 円順列 数学A 場合の数と確率 順列【授業案】立命館守山中学校・高等学校 森園 崇司
| 学年 / 教科 | 高1/数学 |
| 単元 | 数学A 場合の数と確率 順列 |
| 指導要領 | 数学A 場合の数と確率 イ (ア) |
| 教科書会社 | 数研出版 NEXT数学A |
| 授業者 | 森園 崇司(立命館守山中学校・高等学校) |
単元の一部
解説動画
作成者からのアピールポイント
円順列の問題に対するアプローチ方法を、具体的に書き並べたところから導き出す過程にグループでの活動を取り入れた。
この授業案のインポート用ノートデータ
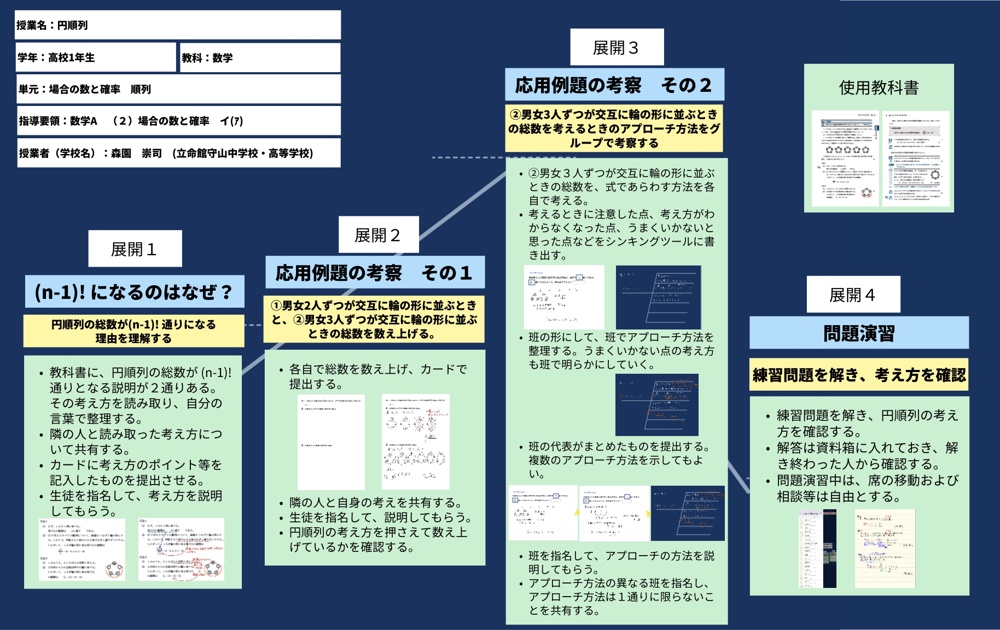
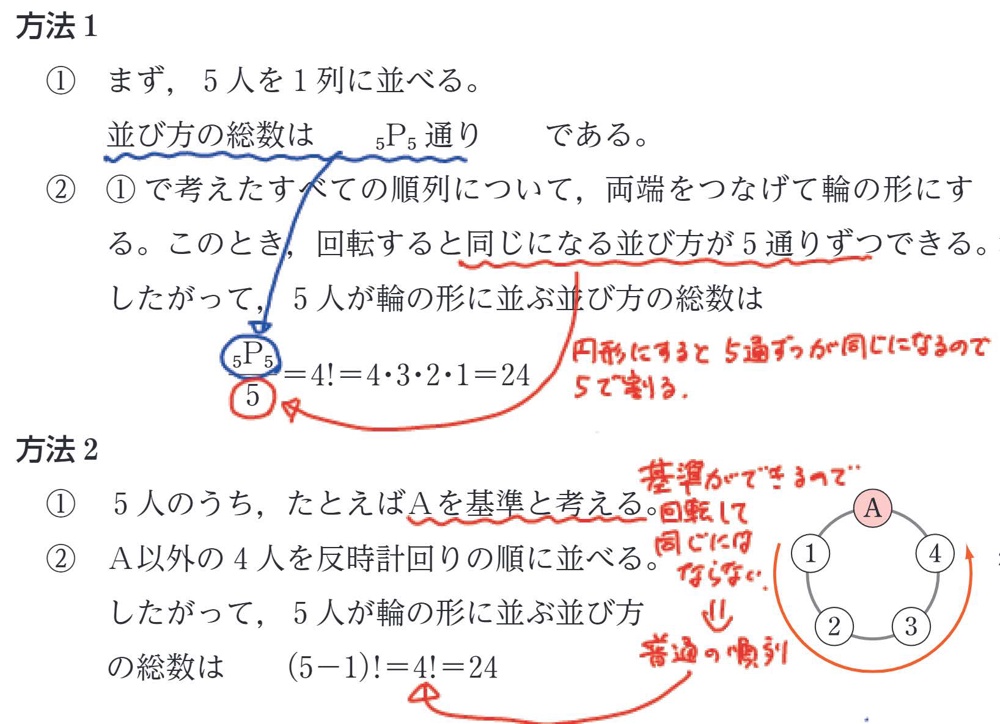
【展開1】(n-1)!になるのはなぜ?
・教科書に書かれている円順列についての説明を各自で読み取る。
・円順列の総数が(n-1)!通りとなる2通りの説明を、自分の言葉で説明できるように整理する。
・読み取った内容を隣の生徒およびクラスの生徒と共有する。

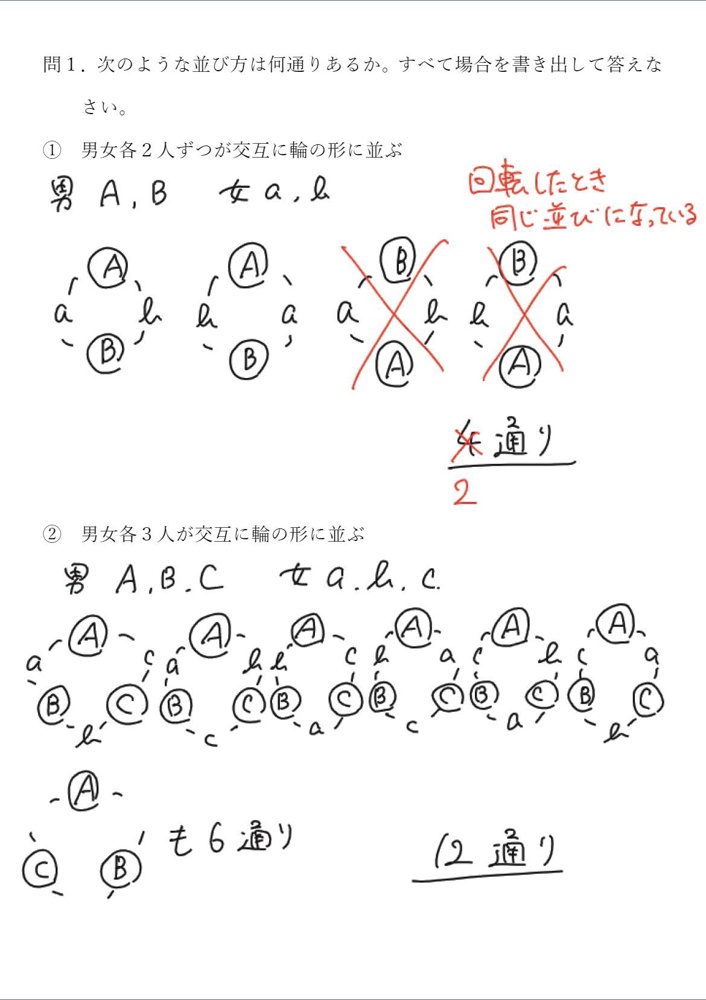
【展開2】応用例題の考察 その1
・①と②の並べ方を実際に書き並べて、数え上げる。
・「回転したときに同じ並びになるものは同じ並び方とみなす」という円順列のポイントを押さえて数え上げていることを確認する。

【展開3】応用例題の考察 その2
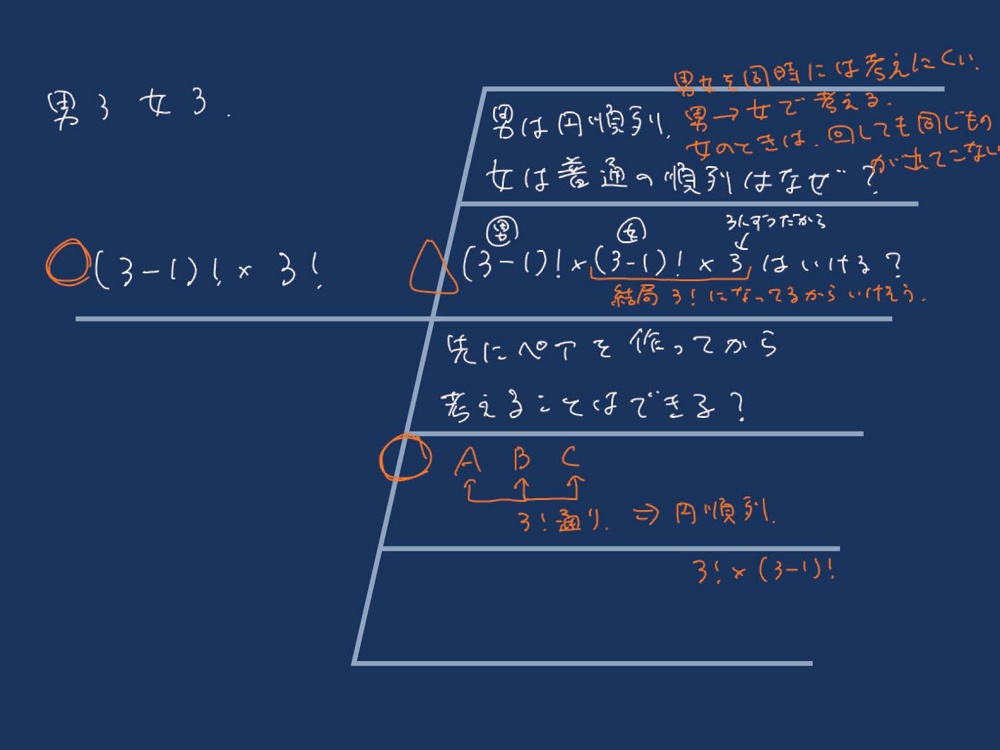
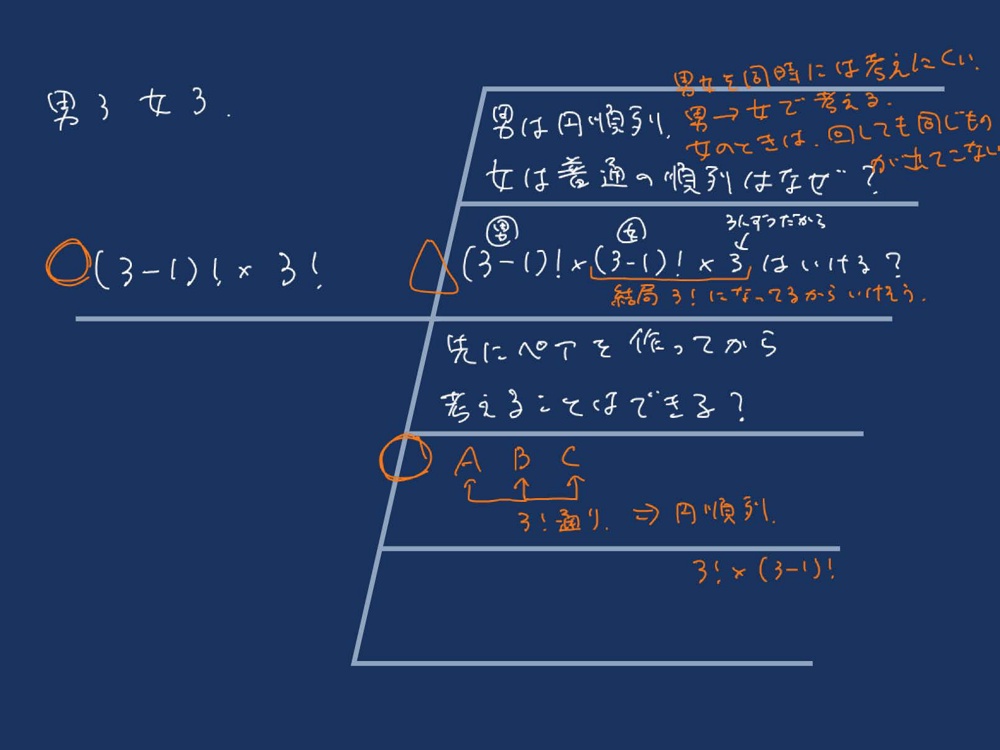
・展開2で数え上げた②について、並べ方の総数を計算式を用いて求める方法を考える。注意した点や、うまくいかずに困った点などは、シンキングツールに書き出す。
・班の中で、アプローチ方法を整理する。このとき、個人で考えてうまくいかなかった点なども共有し、検討する。
・班で考えた内容を代表者に提出してもらう。複数のアプローチ方法や最後まで疑問が残った点についても示してもらう。
・班の代表者に説明してもらい、クラス全体で検討する。特に、アプローチ方法は1通りに限らないことを共有する。




【展開4】問題演習
・練習問題を解き、円順列の問題に対するアプローチ方法を確認する。