高1 数学 円順列の総数の求め方を考えよう 順列【授業案】藤村女子高等学校 小田島 由佳
| 学年 / 教科 | 高1/数学 |
| 単元 | 順列 |
| 指導要領 | 場合の数と確率 ア場合の数(イ) |
| 教科書会社 | 数研出版 新編 数学A |
| 授業者 | 小田島 由佳(藤村女子高等学校) |
単元の一部
解説動画
作成者からのアピールポイント
円順列の総数は(n-1)!で求めることができるのはなぜかを考えるために、実際の塗り分けを分類する過程を大切にしました。
この授業案のインポート用ノートデータ
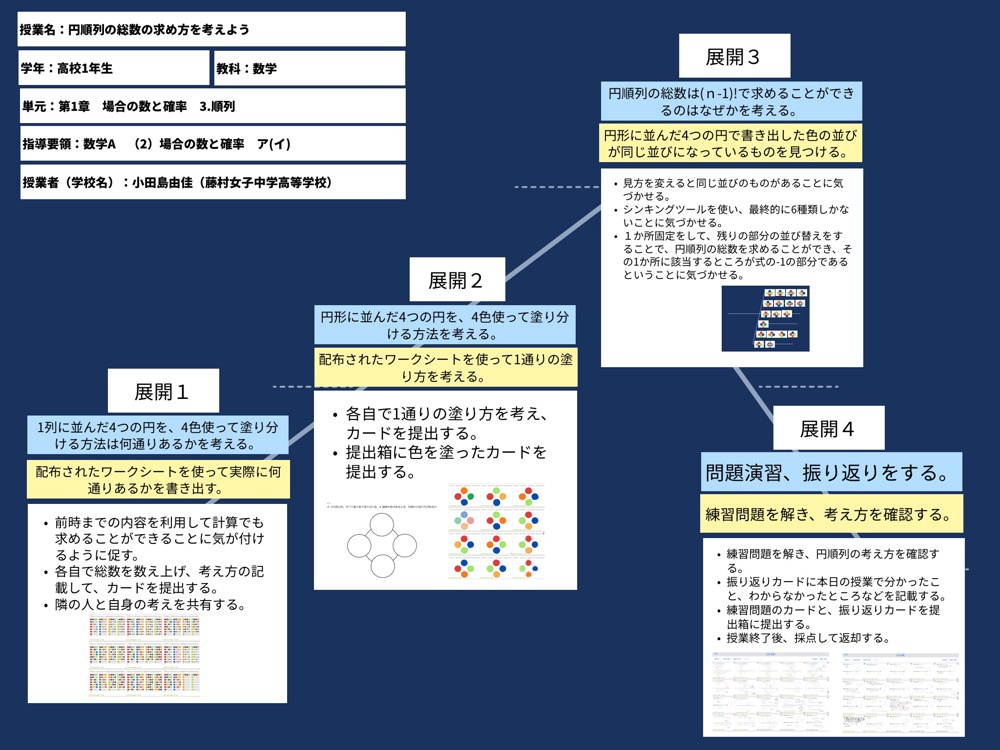
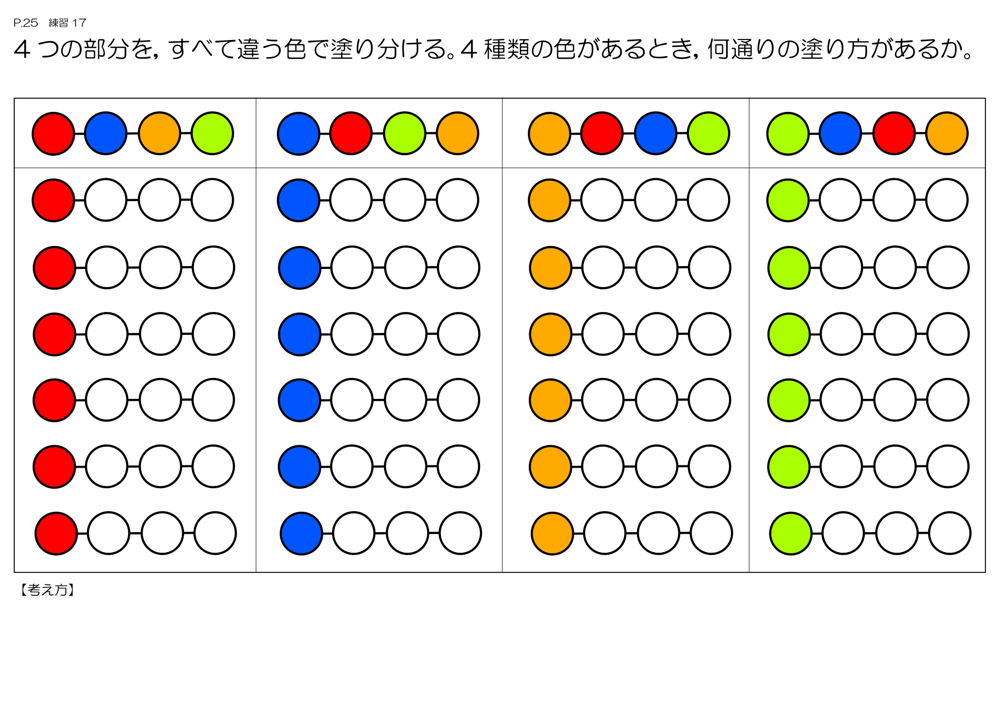
【展開1】1列に並んだ4つの円を、4色使って塗り分ける方法は何通りあるかを考える
前時までの内容を利用して計算でも求めることができることに気が付けるように促す。
各自で総数を数え上げ、考え方の記載して、カードを提出する。
隣の人と自身の考えを共有する。
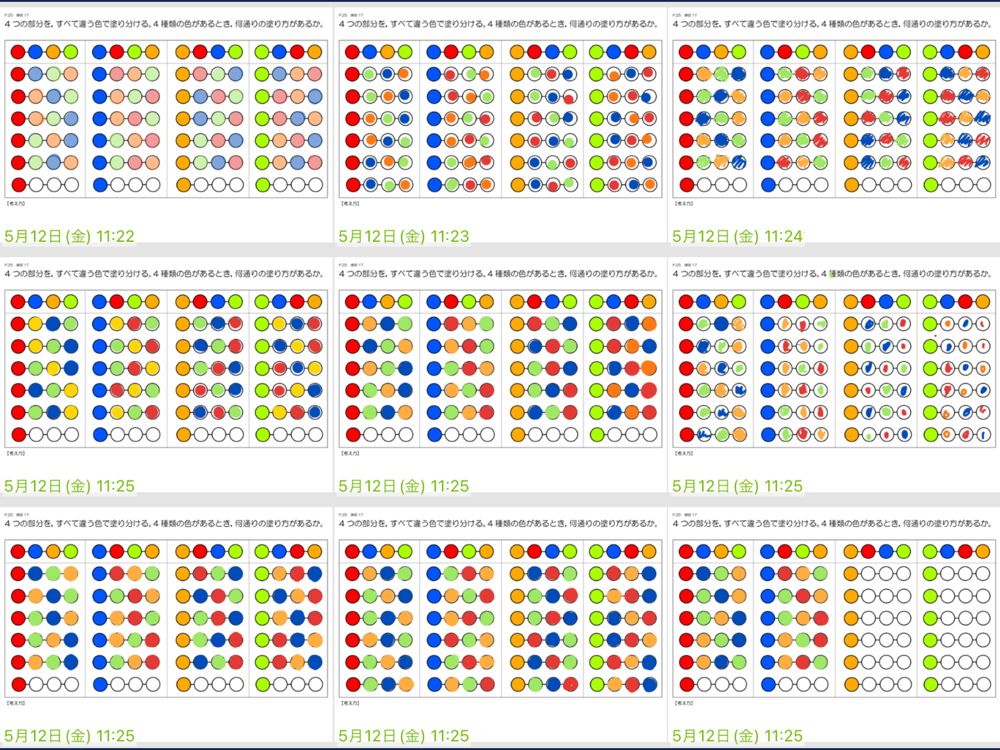
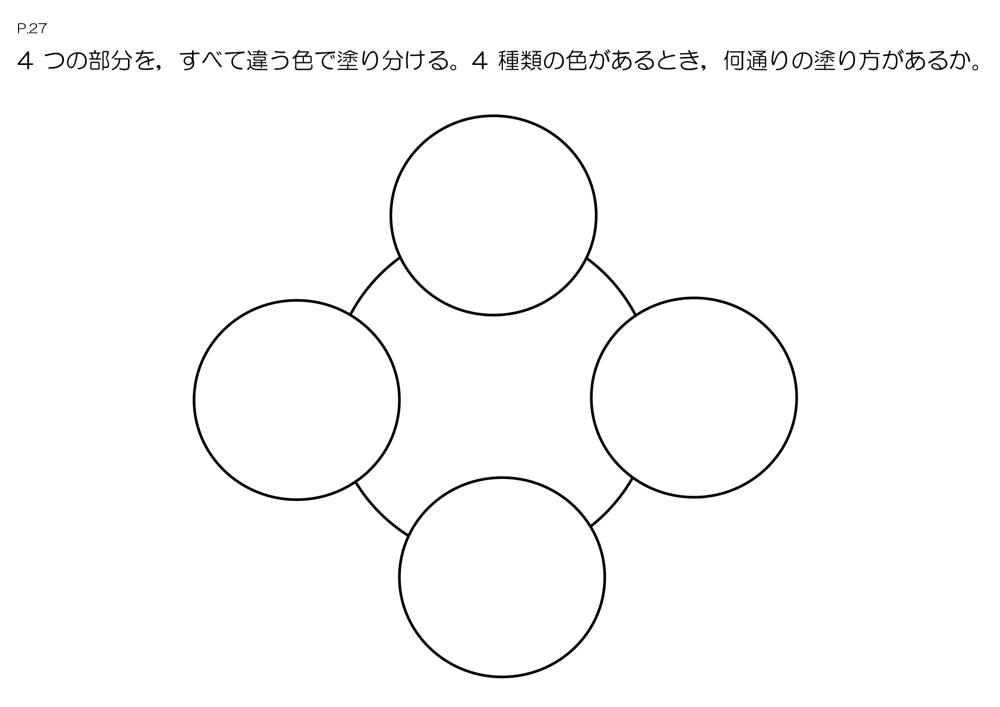
【展開2】円形に並んだ4つの円を、4色使って塗り分ける方法を考える
各自で1通りの塗り方を考え、カードを提出する。
提出箱に色を塗ったカードを提出する。
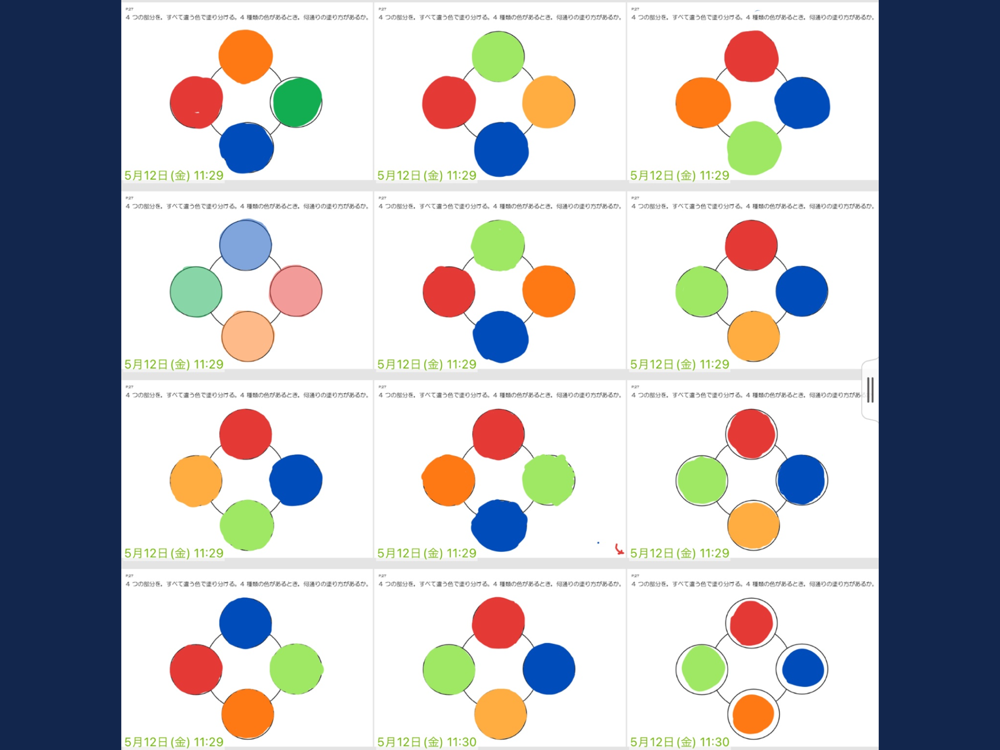
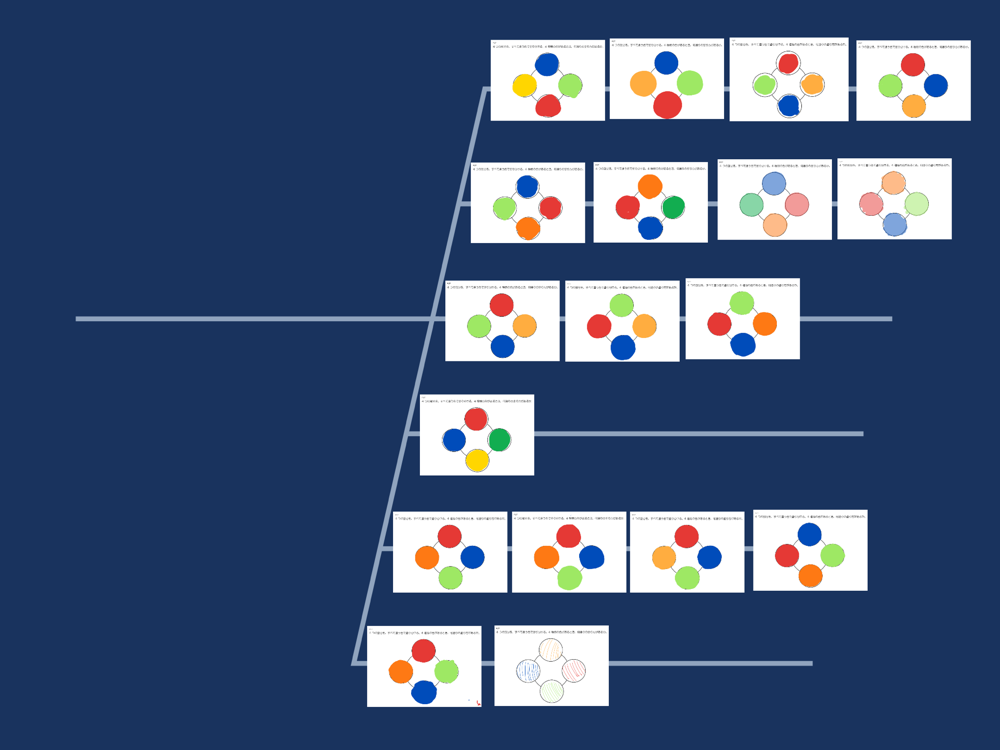
【展開3】円順列の総数は(n-1)!で求めることができるのはなぜかを考える
見方を変えると同じ並びのものがあることに気づかせる。
シンキングツールを使い、最終的に6種類しかないことに気づかせる。
1か所固定をして、残りの部分の並び替えをすることで、円順列の総数を求めることができ、その1か所に該当するところが式の-1の部分であるということに気づかせる。
【展開4】問題演習、振り返りをする
練習問題を解き、円順列の考え方を確認する。
振り返りカードに本日の授業で分かったこと、わからなかったところなどを記載する。
練習問題のカードと、振り返りカードを提出箱に提出する。
授業終了後、採点して返却する。

