高1 数学 証明してみよう! 図形の性質【授業案】立命館守山中学校・高等学校 増井洸介
| 学年 / 教科 | 高1/数学 |
| 単元 | 図形の性質 |
| 指導要領 | 第2章各科目第4節数学A |
| 教科書会社 | NEXT数A |
| 授業者 | 増井洸介(立命館守山中学校・高等学校) |
単元全体
解説動画
作成者からのアピールポイント
私はICTの利点は「動的理解」「同時アクセス性」だと思っています。そしてその上でロイロノートの利点は「提出箱に入れたら、生徒全員が他人の解答を見られる」という同時アクセス性だと思っています。
そこで、geogebraを使うことでアニメーションとしての理解ができるので、ICTの利点を活かせると思っています。
ロイロノートを使って何がしたいかというより、何かしたいことがあってその達成にロイロノートが向いている。という使い方をしていきたいです。
この授業案のインポート用ノートデータ
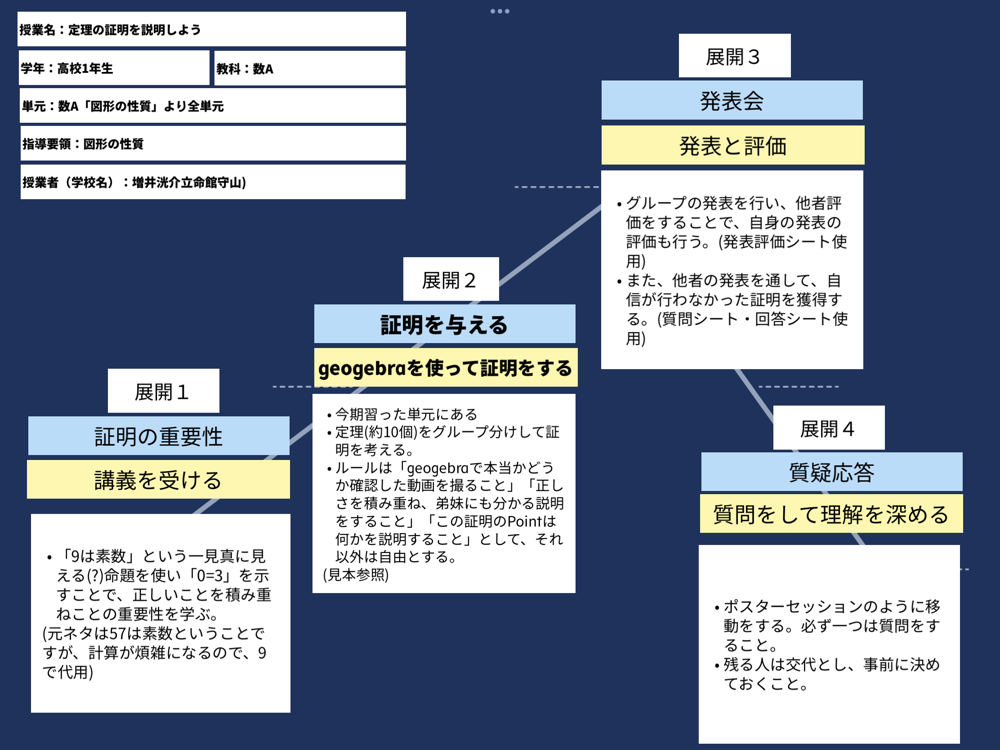
【展開1】証明の重要性
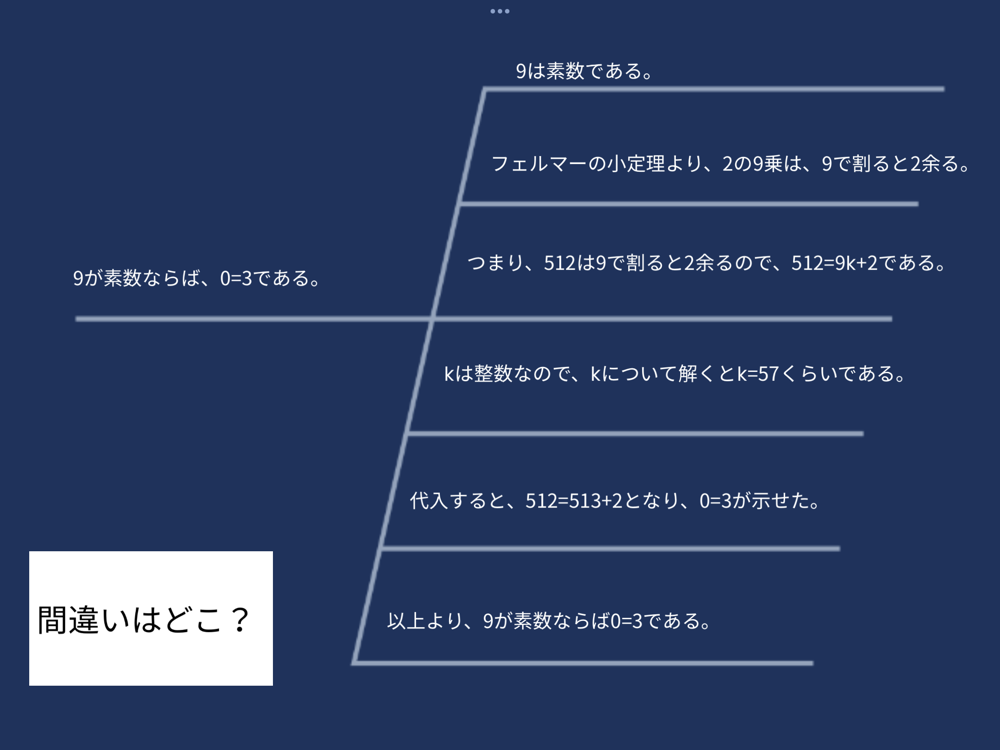
「57は素数」という真に見えてしまう偽の命題から、「0=1」という誤った答えが出てしまうことを用いて、これまでさまざまな定理で長さを求める・角度を求める営みをしてきたが、それが正しいかどうかは別の問題である。定理が正しいことを証明しなければならない。ということを説明する。
2の57乗を計算するのは大変なのでここでは「9は素数」として、妥協してもらう。
【展開2】証明を与える
24人を6グループに分けてそれぞれ重複がないよう(同じ定理の逆の場合は認める)証明をする。注意したいのは、証明そのものに繋がらないけれども「GeoGebraでその定理が本当に正しいんだろう」という動画を添付させることである。この営みを挟むことで、証明に対する糸口が掴めるものもあるし、図形に描写するのは意外と知識を要求されるので、入れている。
「geogebraを使用すること」「弟や妹がいても理解してもらえる説明をすること」「この照明の一番のミソがどこか明言すること」を条件として、それ以外は自由に任せることにする。


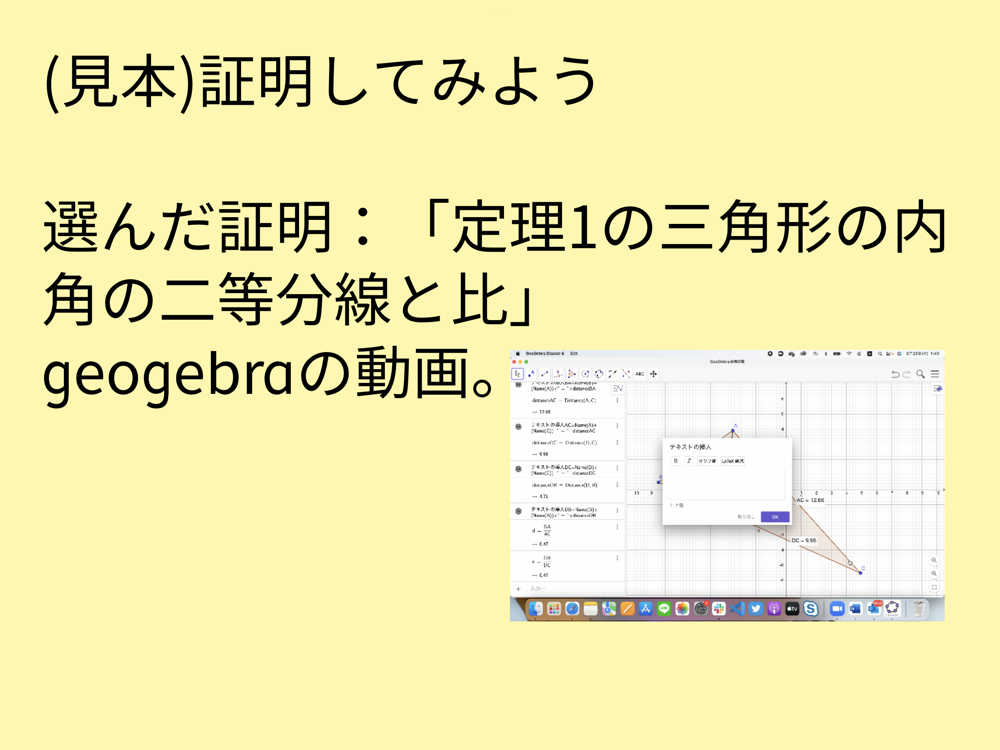
【展開3】発表と評価
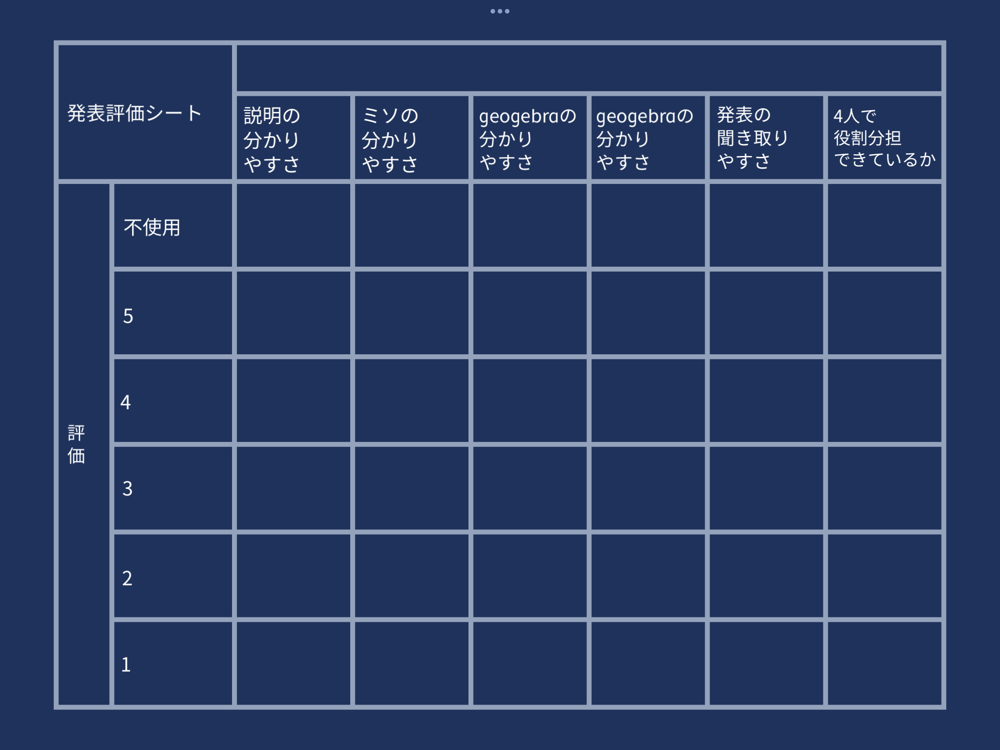
発表前に「評価項目」が書かれた評価シートと、質問シートを配布する。全員一つは質問を用意することで、より積極的な発表になることが期待される。また、何に気をつけて話せばいいのかが目に見えるだろう。

【展開4】質疑応答
展開3での質問をポスターセッションのようにして回答してもらう。答えがわかったかどうかではなく、自らの発表を受け取った人がどう捉えているのか。自分の疑問をどう説明すれば相手に分かってもらえるのか。というところを考える礎にしたい。