高1 数学 不定方程式 整数の性質【授業案】 多治見西高等学校 野呂 利加
| 学年 / 教科 | 高1/数学 |
| 単元 | 整数の性質 |
| 指導要領 | 数学と人間の活動 イ (ア) |
| 教科書会社 | 新編 数学A |
| 授業者 | 野呂 利加(多治見西高等学校) |
単元の一部

解説動画
作成者からのアピールポイント
共有ノートで生徒同士が学びふ深め合う。
新幹線の座席を用いて,現実的な内容から数学的な考え方まで発展させる。
この授業案のインポート用ノートデータ
【展開1】図や表を用いて不定方程式を考える
新幹線の座席を用いて、ロイロでシートを配布して実際に図を用いて移動させることでどのよな座り方があるのかを探す。
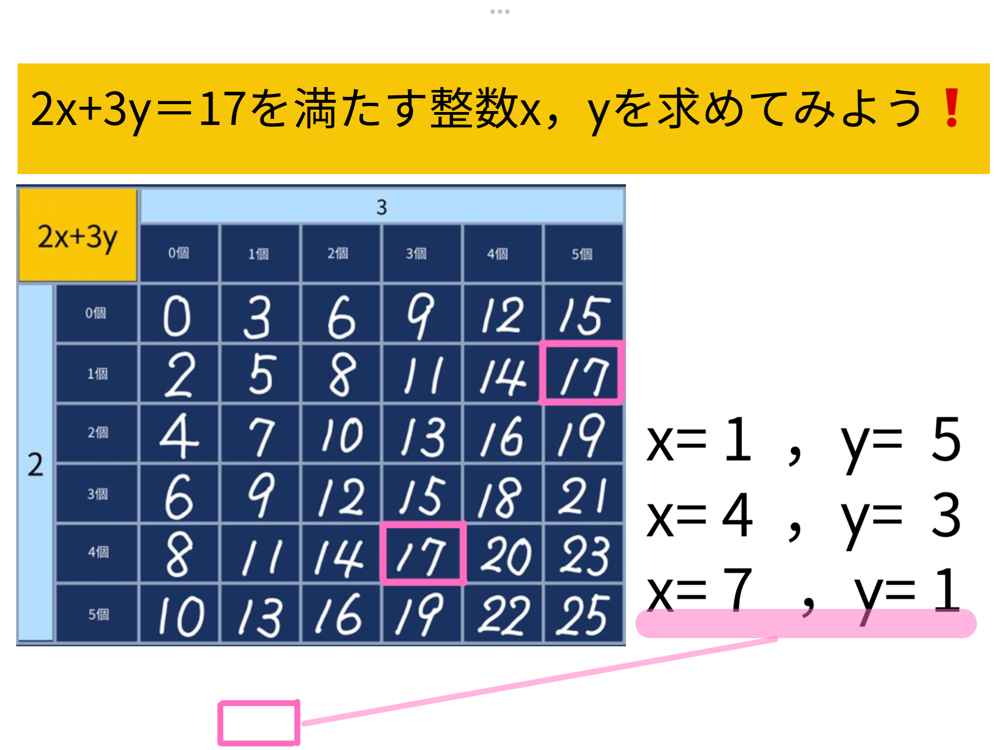
文字式2x+3yを活用して17人のとき、方程式2x+3y=17のX,yの値を表を使って求める。
【展開2】数学的に不定方程式を考える
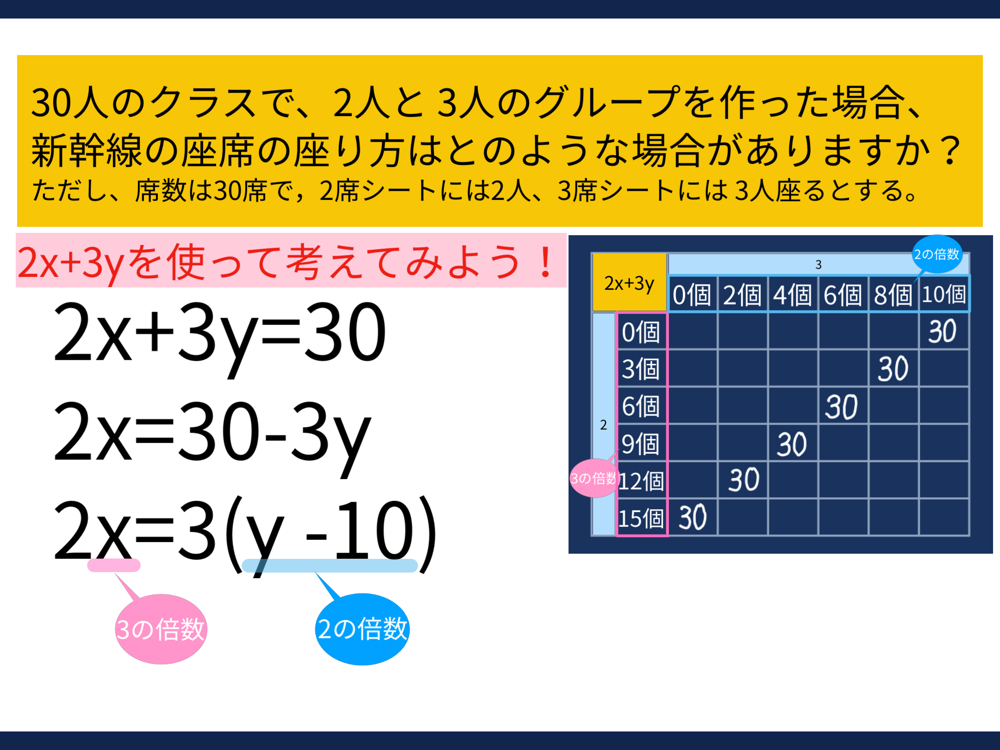
方程式2x+3y=30を変形して、x,yが何の倍数になるのかを見つけることで、x,yの値を導きやすくなることを理解する。
表を活用してx,yの値を求める。

【展開3】複数の不定方程式を解く
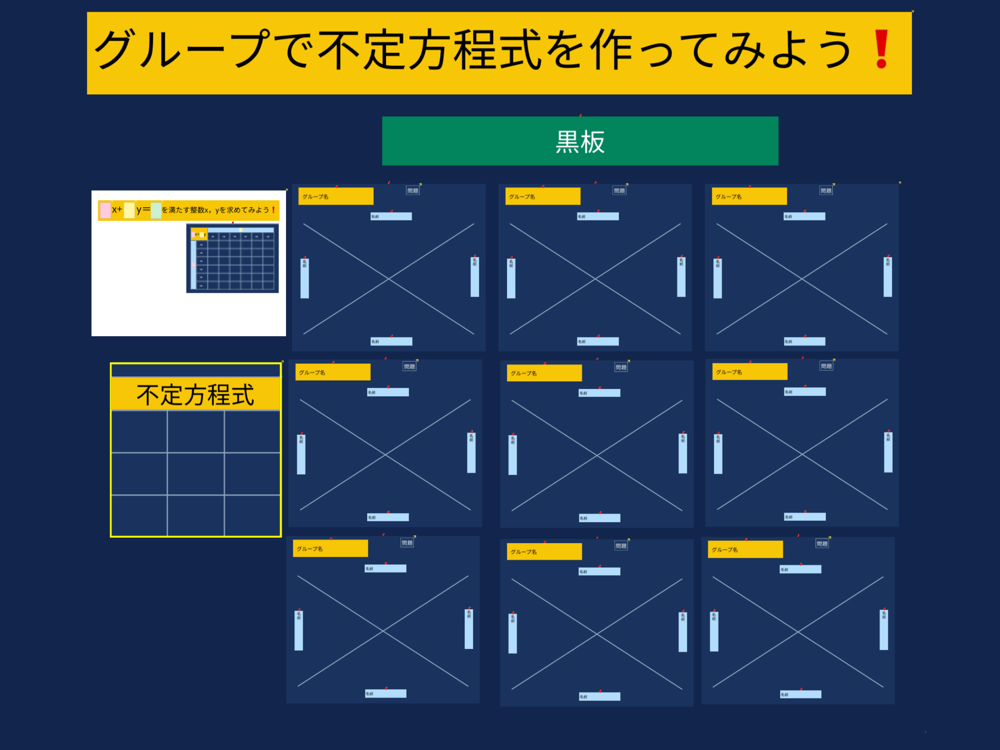
共有ノートを活用して、グループワークする。
グループでa,b,cに数字を当てはめて不定不定式を作り、整数x,yの値を求める。
作成した不定方程式を共有ノート内のシートに提出する。
(グループで複数の不定方程式を提出でき,提出した不定方程式のその場で修正しやす苦するため)
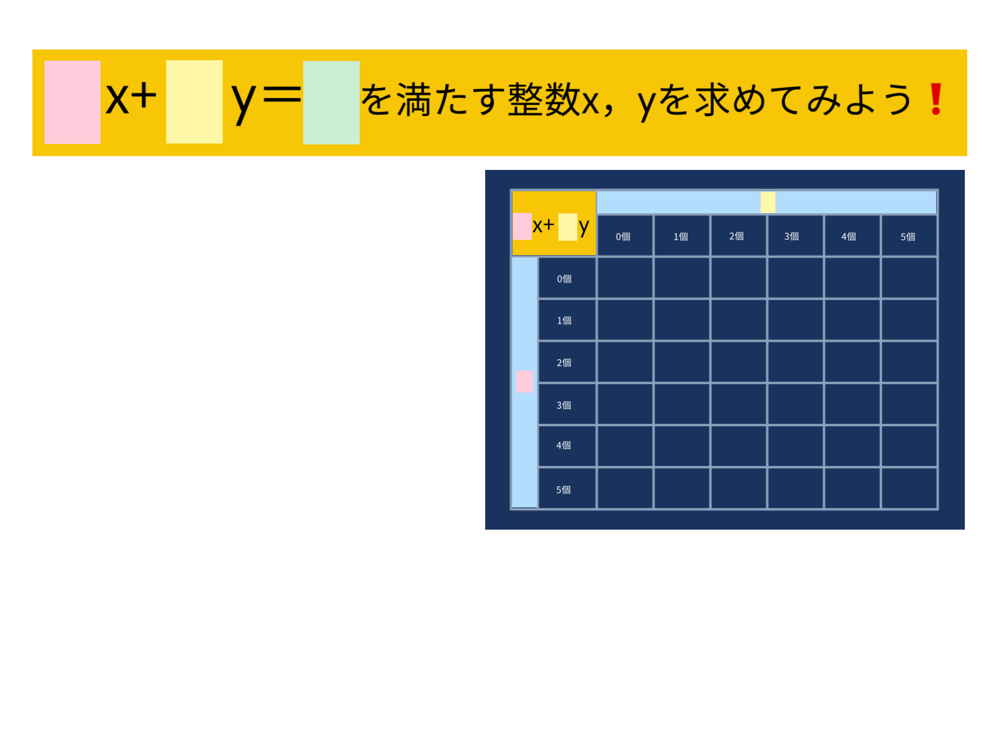
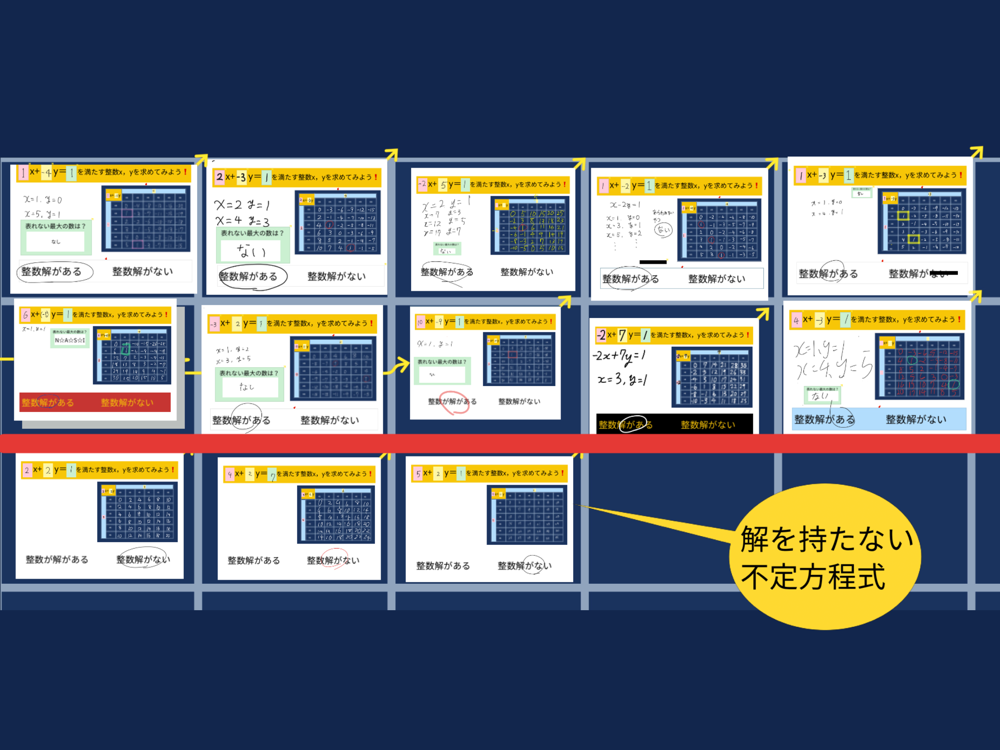
【展開4】不定方程式をの解について考えてみよう
各グループで作成した不定方程式を発表する。
各グループが作成した不定方程式をもとに整数解を持つ場合についてどのような性質があるのかを考える。
不定方程式の性質を見つやすくするために,解を持つ場合と持たない場合を見つけるヒントを用意する。(黒いシートに黒い文字で隠れヒントを用意する。)
生徒はそのヒントから,「2つの整数a,bが互いに素であるとき、ax+by=1を満たす整数x,yが存在する」という性質を見つけた。